[C++ 프로그래머스] 숫자 변환하기

문제 링크

 프로그래머스

1. 문제 설명

1-1. 문제 설명

자연수 x를 y로 변환하려고 합니다. 사용할 수 있는 연산은 다음과 같습니다.

• x에 n을 더합니다
• x에 2를 곱합니다.
• x에 3을 곱합니다.
• 자연수 x, y, n이 매개변수로 주어질 때, x를 y로 변환하기 위해 필요한 최소 연산 횟수를 return 하도록 solution 함수를 완성해 주세요. 이때 x를 y로 만들 수 없다면 -1을 return 해주세요.

1-2. 제한사항

• 1 ≤ x ≤ y ≤ 1,000,000
• 1 ≤ n < y

1-3. 입출력 예

x	y	n	result
10	40	5	2
10	40	30	1
2	5	4	-1

---

2. 문제 풀이

문제 접근법을 자세하게 작성하였습니다.
전체 코드는 짧아 코드로도 이해가 가능하신 분들은 패스하시고 코드만 보셔도 됩니다.

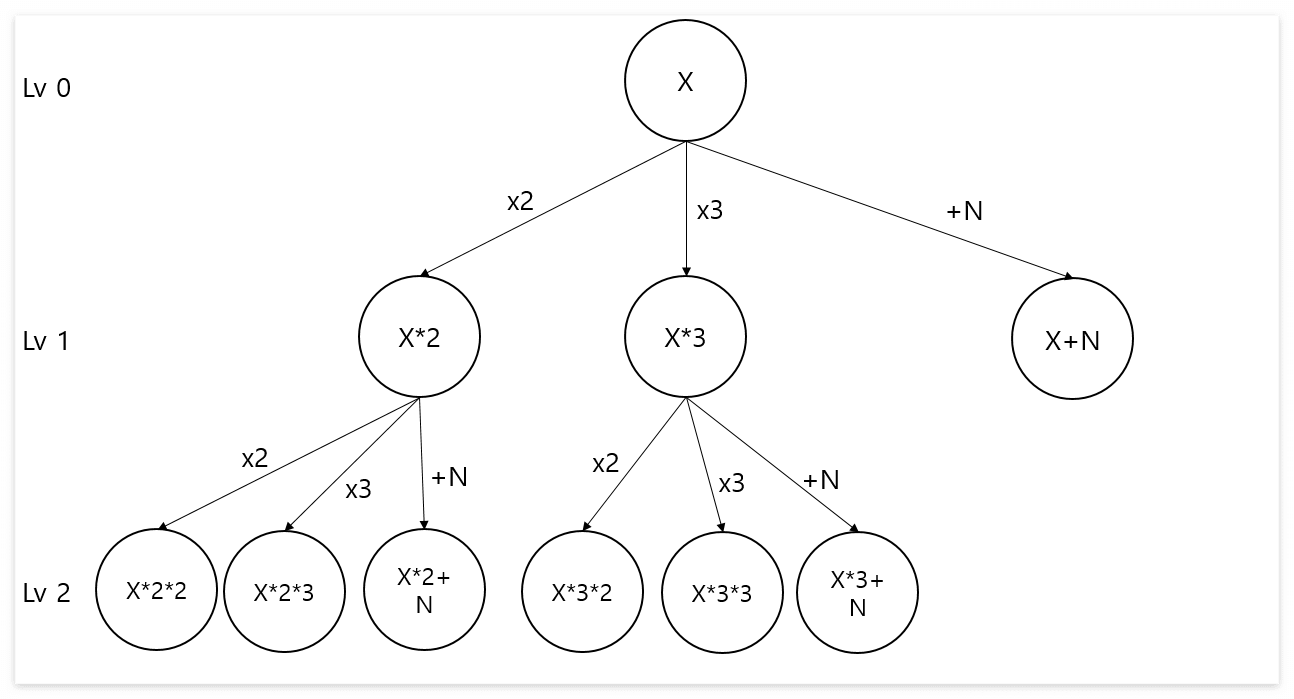
자연수 X에다가 총 3가지의 연산을 해야 한다.

그리고 그 결과 값을 기준으로 또 3가지 연산을 해서 Y로 변환이 될 때까지 진행을 해야 한다.

이런 문제는 DFS, BFS로 풀면 금방 풀 수 있다.

그림을 통해 접근 방법을 이해해보자!!

Lv N의 N은 연산 처리 횟수를 뜻한다.

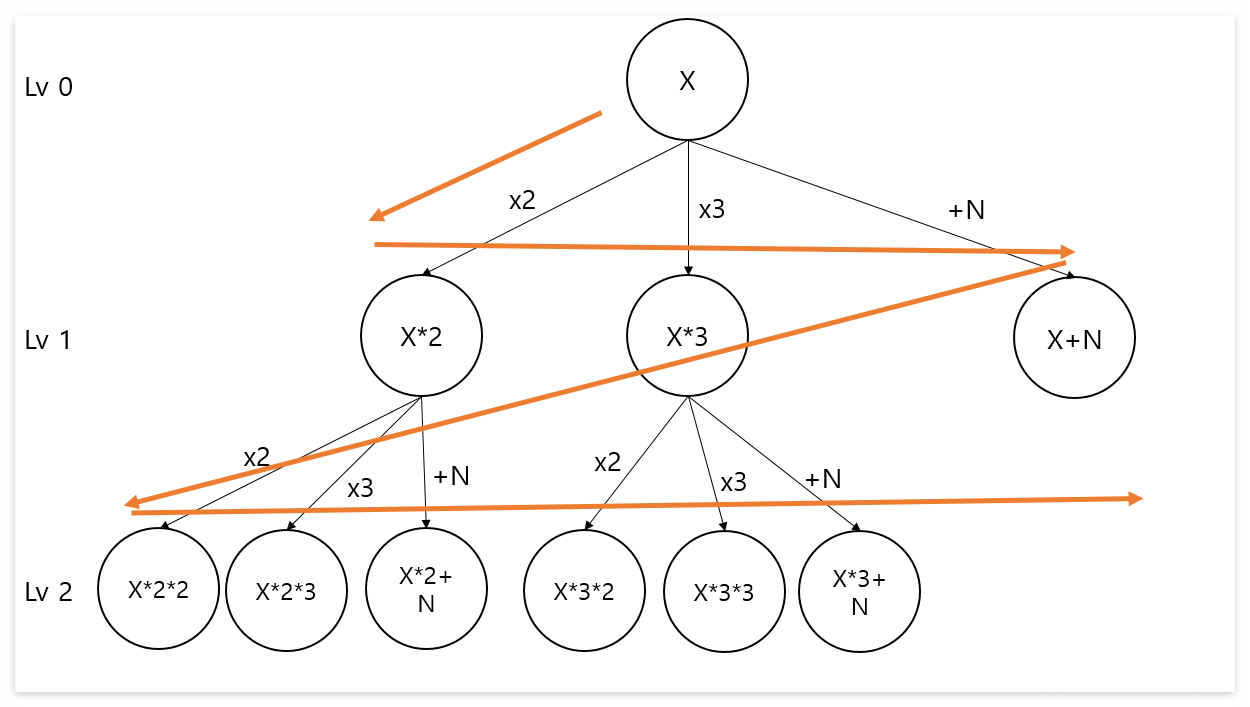
(DFS보단 BFS를 더 선호하기 때문에) 위 그림을 토대로 BFS로 풀어보자.

BFS로 풀기 위해 Queue를 이용할 것이고 Queue에 아래 주황색 화살표처럼 데이터를 저장할 것이다.

Queue에 데이터를 넣을 때 몇 가지 주의해야 할 점이 있는데 하나씩 살펴보자.

2-1. 데이터가 Y보다 큰 경우

주의점 중 하나는 “데이터가 Y보다 큰 경우“이다.

이러면 더 이상 진행할 필요가 없기 때문에 데이터 삽입을 할 필요가 없다.

2-2. 데이터의 맞는 Lv 찾기

두 번 째는 데이터의 맞는 Lv 찾기이다.

이건 풀이 방법마다 다를 순 있지만 필자의 경우는 Queue에서 데이터를 하나 꺼낸 후에 연산을 하고 그 결과 값을 Queue에 다시 넣어주었다.

이렇게 되면 데이터에 해당하는 Lv를 찾기가 어려운데 이를 해결하기 위해서 pair<int,int>(first: data \, second: Lv)를 사용하였다.

2-3. 중복 데이터 피하기

마지막으로는 “중복 데이터 피하기”이다.

이 내용을 보지 않고 BFS를 구현했다면 “시간 초과“가 발생했을 것이다. 이유는 이미 탐색한 데이터를 또 탐색하기 때문이다.

예를 들어,
X: 10 N: 10이라고 가정하자
연산 처리를 진행하면 아래와 같이 된다.
X * 2 = 20
X + N = 20
X * 20에서 이미 20을 구했는데 X + N에서 또 20을 탐색하는 것은 의미 없는 행동임을 알 수 있다.
그러므로, 이미 Queue에 들어간 데이터는 Queue에 삽입하지 않아야 한다.

이를 위해 set <int>를 사용했다.

---

3. 전체 코드

#include <string>
#include <vector>
#include <queue>
#include <set>
using namespace std;

int solution(int x, int y, int n)
{
	if (x == y)
		return 0;

	int answer{ 0 };

	// 숫자, Lv(== 횟수)
	queue<pair<int,int>> queue;
	set<int> set;

	set.insert(x);
	queue.push({x,0});

	while (!queue.empty())
	{
		auto data = queue.front();
		queue.pop();

		if (data.first == y)
		{
			answer = data.second;
			break;
		}
		else if (data.first < y)
		{
			int X2 = data.first * 2;
			if (set.insert(X2).second)
			{
				queue.push({ data.first * 2,data.second + 1 });
			}

			int X3 = data.first * 3;
			if(set.insert(X3).second)
				queue.push({ data.first * 3,data.second + 1 });
			
			int AddN = data.first + n;
			if(set.insert(AddN).second)
				queue.push({ data.first + n,data.second + 1 });
		}
	}

	if (answer == 0)
		return -1;

	return answer;
}