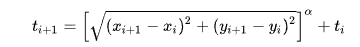유니티 2022 버전에서 스플라인(spline) 기능이 새로 생겼는데 곡선의 종류를 선택하는 것에 베지어 곡선과 캣멀롬 스플라인이 있었다.
베지어 곡선은 근사 곡선인데 반해 캣멀롬 스플라인은 보간 곡선이기 때문에 관심이 생겼고 직접 구현해보면서 정리를 하게 되었다.
1. 캣멀롬 스플라인(Catmull–Rom spline)
한국어 위키 백과보다 영문 위키 백과가 좀 더 자세히 설명되어 있다.
그러므로, 둘 다 살펴보는 것을 추천한다.
Centripetal Catmull–Rom spline - Wikipedia
캣멀롬 스플라인은 컴퓨터 그래픽스 용어로, 에드윈 캣멀과 Raphael Rom에 의해 정의되었다. 출처: 위키백과 - 캣멀롬 스플라인
캣멀롬 스플라인을 검색해보면서 느낀 게 정의가 수학적인 정의만 있다는 것이다.
그렇기 때문에 “캣멀롬 스플라인이 뭐지?”라는 접근 보다
“인접한 두 점을 잇는 곡선을 구현하는 다항식은 다양한데 그중 캣멀롬 스플라인으로 구현하는 방법은 뭐지?”
라고 접근하는 게 맞다고 생각한다.
이를 인지하고 위키 백과를 보면 캣멀롬 스플라인 정의에 대해 아래와 같이 설명하고 있다.
이것을 하나씩 살펴보자.
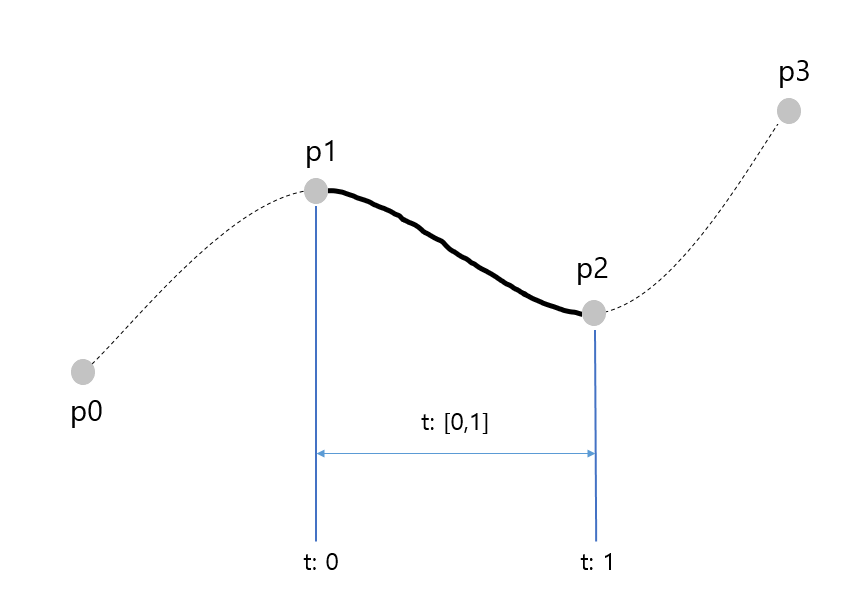
1-1. $t_{0},t_{1},t_{2},t_{3}$ 무엇인가?
곡선이 만나는 점을 의미하고 knot 이라고도 한다.
1-2. t는 무엇인가?
$t_{0},t_{1},t_{2},t_{3}$은 설명이 있지만 t에 대한 설명이 없어서 난감했다.
처음에는 오타인 줄 알았다
몇 가지 의문을 가진 채 실제로 구현해본 결과, 결론은 interpolation value 즉, 보간 값이다.
여기서 보간 값이란
선형 보간법 식에서 나오는 $(1-t)*p1 + t*p2$ 에 t를 의미한다.t를 표현하는 정확한 단어인지는 모르겠으나, 글로 표현하기가 애매해 보간 값이라고 하였다.
그리고 이 값이 표현하는 범위는 $t_{1},t_{2}$ 사이에 생기는 곡선이다.
$t_{1},t_{2}$은 곡선이 만나는 점이며, $t_{1}, t{2}$는 각각 P1, P2에 대응하기 때문이다.
즉,
- t의 범위는 [0,1]
- t = 0 일 때 곡선의 시점
- t =1 일 때 곡선의 종점
이다.
t는 p1,p2 사이에 생긴 곡선의 보간 값이다. 실제 계산에는 $t_{1},t_{2}$를 이용해야 함을 유의하자.
1-2. C는 무엇인가
글에 적혀있듯이 캣멀롬 스플라인은
$C = \frac{t_{2} - t}{t_{2} - t_{1}}B_{1} + \frac{t - t_{1}}{t_{2} - t_{1}}B_{2}$
로 표현한다.
식의 결과 값이 C인데, 식에서 위에서 확인한 t가 존재하는 것을 볼 수 있다.
그러므로, C의 결과는 “t값에 따른 곡선 위를 지나는 점의 위치 값“이라 볼 수 있다.
2. 코드 구현
2-1. $t_{i+1}$ 구하기
1
2
3
4
float GetNextT(float t, Vector2 p0, Vector2 p1)
{
return Mathf.Pow(Vector2.SqrMagnitude(p1 - p0), 0.5f * _alpha) + t;
}
아래의 수식을 코드로 변환한 것이 위의 코드인데 수식을 하나씩 살펴보면서 코드와 연결해 보자.
\[\\sqrt{(x\_{i+1} - x\_{i})^2 + (y\_{i+1} - y\_{i})^2}\]출처: 위키백과(캣멀롬 스플라인)
$(x_{i+1} - x_{i})^2 + (y_{i+1} - y_{i})^2$ 는 피타고라스의 정리에 따라 두 점 사이 거리의 제곱을 의미한다.
그렇기 때문에 Vector2.SqrMagnitude(p1 - p0)로 두 점 사이 거리의 제곱을 구했다.
\[\\sqrt{f(x,y)}\]$\sqrt{f(x,y)}$는 다르게 표현하면 $f(x,y)^{0.5}$ 로도 표현할 수 있다.
이것을 이용해서 아래와 같이 코드로 작성하였다.
1
Mathf.Pow(Vector2.SqrMagnitude(p1 - p0), 0.5f * _alpha)
2-2. C 구하기
2-1 방법을 통해 $t_{0},t_{1},t_{2},t_{3}$ 값은 구했으므로 C 값은 식을 적용하면 바로 구할 수 있다.
여기서 주의해야 할 점이 있는데, 바로 t 값이다.
t 값은 $t_{1},t_{2}$ Knot 사이 곡선들의 보간 값이라고 확인했다.
그러므로, t는 아래와 같이 처리를 해야 한다.
1
2
// interpolationValue: 0 ~ 1 사이의 값
float t = Mathf.Lerp(t1, t2, interpolationValue);
2-3. 전체 코드
위에서 코드를 설명할 때 나오는 _alpha 변수는 3가지 값을 가지고 있기 때문에 ENUM 처리를 하였다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
public class CatmullRomSpline
{
public enum SplineType
{
Uniform,
Centripetal,
Chordal,
}
Vector3 _p0, _p1, _p2, _p3;
SplineType _type;
public CatmullRomSpline(Vector3 p0, Vector3 p1, Vector3 p2, Vector3 p3, SplineType type)
{
(_p0, _p1, _p2, _p3) = (p0, p1, p2, p3);
_type = type;
}
/// <summary>
///
/// </summary>
/// <param name="interpolationValue">0: 곡선의 시점 / 1: 곡선의 종점</param>
/// <returns></returns>
public Vector3 GetPoint(float interpolationValue)
{
float t0 = 0;
float t1 = GetNextT(t0, _p0, _p1);
float t2 = GetNextT(t1, _p1, _p2);
float t3 = GetNextT(t2, _p2, _p3);
float t = Mathf.Lerp(t1, t2, interpolationValue);
Vector3 A1 = (t1 - t) / (t1 - t0) * _p0 + (t - t0) / (t1 - t0) * _p1;
Vector3 A2 = (t2 - t) / (t2 - t1) * _p1 + (t - t1) / (t2 - t1) * _p2;
Vector3 A3 = (t3 - t) / (t3 - t2) * _p2 + (t - t2) / (t3 - t2) * _p3;
Vector3 B1 = (t2 - t) / (t2 - t0) * A1 + (t - t0) / (t2 - t0) * A2;
Vector3 B2 = (t3 - t) / (t3 - t1) * A2 + (t - t1) / (t3 - t1) * A3;
Vector3 C = (t2 - t) / (t2 - t1) * B1 + (t - t1) / (t2 - t1) * B2;
return C;
}
float GetNextT(float t, Vector3 p0, Vector3 p1)
{
return Mathf.Pow(Vector3.SqrMagnitude(p1 - p0), 0.5f * GetAlpha(_type)) + t;
}
float GetAlpha(SplineType type)
{
switch (type)
{
case SplineType.Uniform:
return 0f;
case SplineType.Centripetal:
return 0.5f;
case SplineType.Chordal:
return 1f;
default:
return 0f;
}
}
}
3. 결과 확인하기
결과 확인하기 위해 Gizmo를 사용하였고 제대로 적용되는지를 확인하기 위해 점은 4개로 고정하여 구현하였다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
private void OnDrawGizmos()
{
Gizmos.color = Color.red;
if(_points != null &&
_points.Count > 3)
{
CatmullRomSpline spline = new CatmullRomSpline(_points[0].position,
_points[1].position,
_points[2].position,
_points[3].position,
_splineType);
Vector3 prevP = spline.GetPoint(0);
for (int i = 1; i < _gizmoDetail; i++)
{
Vector3 p = spline.GetPoint((float)i / _gizmoDetail);
Gizmos.DrawLine(prevP, p);
prevP = p;
}
}
}
출처:
위키백과(CC-BY-SA 3.0)