1. 스플라인 곡선
스플라인 곡선(영어: spline curve)은 주어진 복수의 제어점을 통과하는 부드러운 곡선으로, 인접한 두 점 사이에의 구간마다 별도의 다항식을 이용해 곡선을 정의한다.
출처: 위키 백과(스플라인 곡선)
위키 백과 설명 중에 “인접한 두 점 사이에 구간마다 별도의 다항식을 이용해 곡선을 정의한다.”라고 설명이 되어 있는데
설명대로 점이 여러 개 있을 때 인접한 두 점 사이마다 다항식을 이용해 곡선을 만든다.
여기서 인접한 두 점 사이에 적용되는 다항식이 무엇이냐에 따라 다양한 곡선이 나타나게 되는데 앞서 배운 베지어 곡선(Bezier Curve) 또한 다양한 곡선 중 하나라고 볼 수 있다.
그리고 두 점 사이마다 곡선을 구현한 다음에 곡선끼리 연결을 하게 되면 스플라인 곡선이 된다.
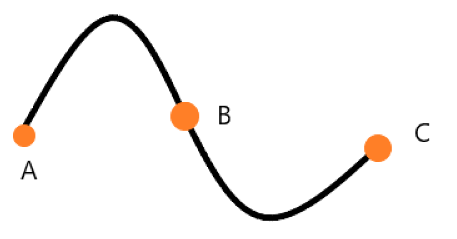
곡선이 연결되는 것이다 보니 당연하게 특정 곡선의 끝점과 다음 곡선의 시작점이 같아야 한다.
점A, B를 연결하는 곡선과 점B, C를 연결하는 곡선
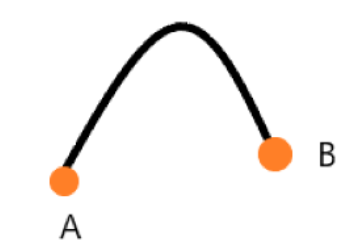

예를 들어,
베지어 곡선을 이용해 인접한 두 점의 곡선을 구현했다고 가정하자.
이 때 구현한 베지어 곡선들을 서로 연결하여 스플라인 곡선을 만들 수 있는데 이것을 복합 베지어 곡선(베지어 스플라인)이라고 한다.
2. 보간 곡선과 근사 곡선
곡선을 찾아보면 보간(Interpolation)과 근사(approximation)라는 단어를 자주 볼 수 있는데 두 개의 차이는 명확하다.
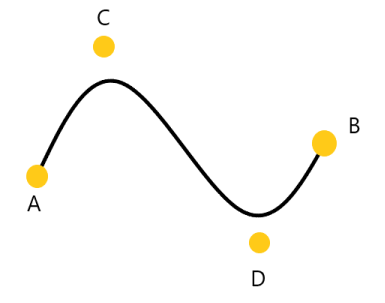
- 보간(Interpolation): 곡선이 중간점을 통과함 (Ex. 캣멀롬 스플라인)
- 근사(approximation): 곡선이 중간점을 통과하지 않고 곡선을 제어하기만 함 (Ex. 베지어 곡선)
3. 연속성(Continuity)
$C^0$
- 두 개의 곡선이 연결된 점이 동일
- 두 개의 곡선 중 하나는 종점, 다른 하나는 시점인데 이것이 동일한지 물어보는 것
$C^1$
- 연결된 점을 기준으로 기울기가 같음
- 두 곡선을 이루는 방정식을 1회 미분한 결과가 같다.
$C^2$
- 연결된 점을 기준으로 기울기와 곡률이 같음
- 두 곡선을 이루는 방정식을 2회 미분한 결과가 같다.
곡률이란? (위키백과: 곡률)
선 또는 공간의 굽은 정도를 표시하는 수치 즉, ‘굽은 정도’를 뜻한다.
곡률이 클수록, 굽어짐이 심하고
곡률이 작을수록, 굽어짐이 약해지는데
위키백과에서는 아래와 같이 설명하고 있다.
==================
‘원’은 그 위의 모든 점에서 반지름의 역수를 곡률로 가진다.
따라서 작은 원은 좀 더 심하게 굽어 있으므로 곡률이 크고, 반대로 원이 커질수록 곡률은 작아진다.
곡선이 $C^2$ 까지 지원하려면 미분을 2회 시행할 수 있어야 하기 때문에 곡선을 이루는 다항식은 3차 방정식이어야 한다.
이러한 3차 방정식으로 이루어진 스플라인을 3차 스플라인이라고 한다.
(보통 3차 스플라인을 주로 사용한다고 한다.)
출처: