[Unity] 베지어 곡선(Bezier Curves) 구현해보기

게임을 개발하다보면 곡선을 그려야 할 때가 자주 있다.

곡선을 그리는 방법이 다양하게 있는데 그 중 베지어 곡선(Bezier Curves)에 대해 알아보자

1. 베지어 곡선이란

점과 점 사이의 선형 보간을 통해 그리는 곡선 이라 볼 수 있다.

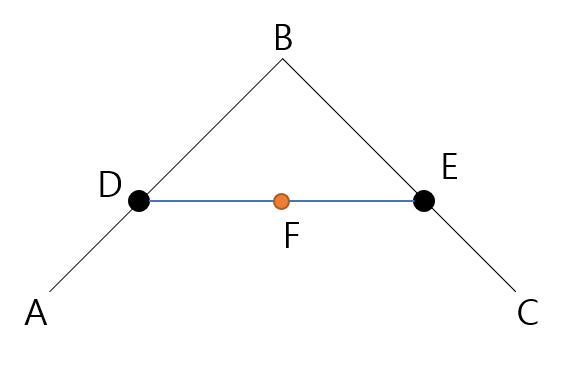
예를 들어, 점 A, B, C가 있을 때

 - A 와 B 의 선형 보간 값 D

 - B 와 C 의 선형 보간 값 E

 - D 와 E 의 선형 보간 값 F

이 있다고 가정하자.

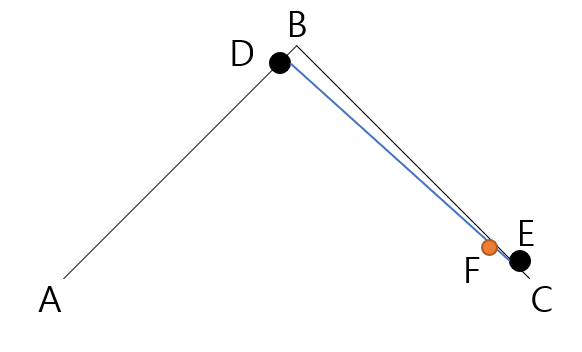
여기서 선형 보간의 수식인 $(1-t)*p1 + t*p2$ t = [0,1] 에 따라 t가 0에서 1로 갈 때 아래와 같이 점 F가 이동할 것이다.

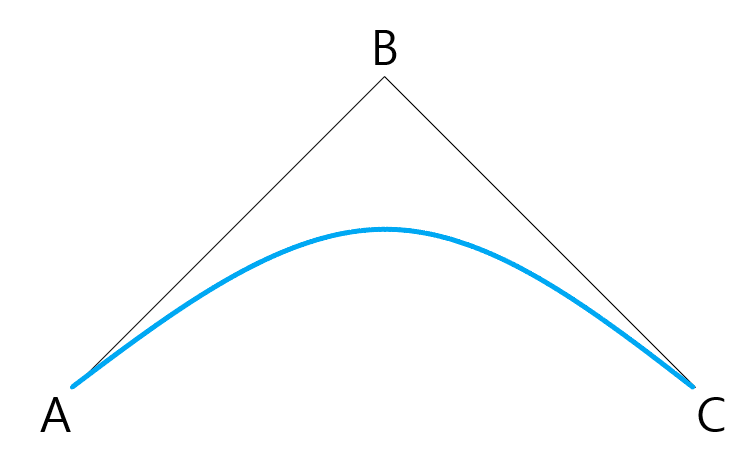
t의 변화량에 따른 점 F의 변화를 선으로 보면 아래와 같이 곡선으로 연결된 것을 볼 수 있다.

이것이 바로 선형 보간을 이용한 베지어 곡선이다.

그리고 위 그림을 통해 하나의 사실을 알 수 있는데 베지어 곡선은 시작과 끝을 제외한 중간점(Ex. B)을 지나치지 않는다.

2. 구현

이론을 알아보았으니 이제 유니티를 통해 구현해보자.

유니티에서는 선형 보간을 Lerp 라는 메소드명으로 지원하고 있다. 그러므로 이를 통해서 베지어 곡선을 구현해보자.

아래 코드는 구현된 베지어 곡선의 경로를 _target 객체가 계속 이동하는 코드이다.

이론을 이해했다면 코드 또한 이해가 가능할 것이기에 코드에 대한 설명은 생략한다.

public class BezierCurves : MonoBehaviour
{
    public Transform _target;
    public Transform _p1,_p2,_p3;
    public float _duration;

    private void Start()
    {
        StartCoroutine(COR_BezierCurves());
    }

    IEnumerator COR_BezierCurves(float duration = 1.0f)
    {
        float time = 0f;

        while(true)
        {
            if (time > 1f)
            {
                time = 0f;
            }

            Vector3 p4 = Vector3.Lerp(_p1.position, _p2.position, time);
            Vector3 p5 = Vector3.Lerp(_p2.position, _p3.position, time);
            _target.position = Vector3.Lerp(p4, p5, time);

            time += Time.deltaTime / duration;

            yield return null;
        }
    }
}

2-1. Gizmos 를 통해 확인하기

Gizmos 를 통해 실제 경로가 어떻게 되는지 확인해보자.

t 값에 따른 점 F의 위치 값을 List에 저장한 후 각 위치 값들을 Gizmo.DrawLine을 통해 선으로 연결해주는 코드이다.

public class BezierCurves : MonoBehaviour
{
    public Transform _target;
    public Transform _p1,_p2,_p3;
    public float _gizmoDetail;

    List<Vector3> _gizmoPoints = new List<Vector3>();
    private void OnDrawGizmos()
    {
        _gizmoPoints.Clear();

        if (_p1 != null && _p2 != null && _p3 != null && _gizmoDetail > 0)
        {
            for (int i = 0; i < _gizmoDetail; i++)
            {
                float t = (i / _gizmoDetail);
                Vector3 p4 = Vector3.Lerp(_p1.position, _p2.position, t);
                Vector3 p5 = Vector3.Lerp(_p2.position, _p3.position, t);
                _gizmoPoints.Add(Vector3.Lerp(p4, p5, t));
            }
        }

        for (int i = 0; i < _gizmoPoints.Count - 1; i++)
        {
            Gizmos.DrawLine(_gizmoPoints[i], _gizmoPoints[i + 1]);
        }
    }
}

코드를 적용하면 아래와 같이 Scene 뷰에서 기즈모가 노출되는 것을 볼 수 있다.

3. 결과

베지어 곡선으로 만들어진 기즈모 라인에 따라 구가 이동하는 것을 볼 수 있다.