구면 좌표계 구현해보기

“유니티로 배우는 게임 수학” 책을 읽다가 구면 좌표계에 대해 알게 되었다.

구면 좌표계는 몰랐던 내용이었는데 읽으면서 내용이 흥미로웠고 간단한 테스트를 해본 내용을 정리하였다.

해당 글은 위키백과: 구면 좌표계 문서를 기반으로 공부한 내용을 정리하였습니다.
그러므로, 아래 글을 읽기 전에 문서를 읽고 오심을 추천드립니다.

0. 시작하기 앞서

필자는 구면 좌표계는 이론일 뿐이고 이걸 어떻게 활용하냐가 중요하다고 생각한다.
그러므로 한 결과물을 다양한 방법으로 구현할 수 있을뿐더러 다양한 결과물을 만들어 낼 수 있음을 참고하자

구면 좌표계를 이용해서 어쌔신 크리드 게임에서 자주 나오는 동기화 화면을 만들 것이다.

assassin’s creed synchronization이라고 검색하면 많은 자료를 볼 수 있다.

만드는 방법을 설명하면 구면 좌표계를 적용할 타켓 객체를 파라미터로 전달받아 구면 좌표계를 통해 원점을 중심으로 한 바퀴를 돌릴 것이다.

위키 백과에서 설명을 보았으면 주의해야 할 사항이 하나 있다.
구면 좌표계 위키 백과를 보면
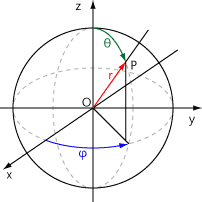
구면 좌표계를 아래와 같이 표현하고 이를 기준으로 설명하고 있는데 유니티와 좌표축이 다르다.
위키 백과에서 설명하는 **y 축은 유니티에서 z 축이고, z 축은 유니티에서 y축이다. 이 점을 유의해서 보자.
그리고 각도를 Φ와 Θ로 표시했는데 Φ는 Azimuth(방위각) Θ는 Elevation(앙각)으로 변수명을 작성하였다.
**

1. 생성자 구현

필자는 생성자를 통해 아래 4가지를 초기화했다.

구면 좌표계를 적용할 타켓
방위각의 최소 최대 각도
앙각의 최소 최대 각도
반지름 길이

  
public class SphericalCoordinate
{
    float _radius;
    Transform _target;
    float _azimuth, _maxAzimuthAngle, _minAzimuthAngle; // 방위각
    float _elevation, _maxElevation, _minElevation;     // 앙각

    public float Azimuth
    {
        get { return _azimuth; }
        set { _azimuth = Mathf.Clamp(value, _minAzimuthAngle, _maxAzimuthAngle); }
    }

    public float Elevation
    {
        get { return _elevation; }
        set { _elevation = Mathf.Clamp(value, _minElevation, _maxElevation); }
    }
    
    public SphericalCoordinate(Transform target, float radius, (float min, float max) azimuth, (float min, float max) elevation)
    {
        _target = target;
        _minAzimuthAngle = azimuth.min * Mathf.Deg2Rad;
        _maxAzimuthAngle = azimuth.max * Mathf.Deg2Rad;
        _minElevation = elevation.min * Mathf.Deg2Rad;
        _maxElevation = elevation.max * Mathf.Deg2Rad;

        _radius = radius;

        Azimuth = Mathf.Atan2(_target.transform.position.z, _target.transform.position.x);
        Elevation = Mathf.Acos(_target.transform.position.y / _radius);
    }
}

여기서 유심히 봐야 할 것은 방위각과 앙각의 최소 최대 각도에 Mathf.Deg2Rad를 곱해준 것이다.

이유는 유니티에서 제공해 주는 Mathf 구조체에 있는 삼각함수 공식들의 반환값은 라디안 값이기 때문이다.

UnityEngine의 Mathf 구조체 안에 삼각함수 정의 중
Atan2를 보면 아래와 같이 반환 값은 라디안 각도로 반환되는 것을 볼 수 있다.

  
    //
    // 요약:
    //     Returns the angle in radians whose Tan is y/x.
    //
    // 매개 변수:
    //   y:
    //
    //   x:
    public static float Atan2(float y, float x);

방위각(Azimuth)과 앙각(Elevation) 계산에 삼각 함수 공식이 들어갔는데 위키 백과에 적혀 있는 좌표 변환 내용을 그대로 가져온 것이다.

\[\\theta=\\arccos(\\dfrac{y}{r})\] \[\\phi=\\arctan(\\dfrac{z}{x})\]

위에서도 말했지만 주의해야 할 점은
위키 백과에서 y축은 유니티에서 z 축, z 축은 유니티에서 y축이다.
잊지 말자!!

2. 구면 좌표계에서 직교 좌표계로

생성자를 통해 구면 좌표계에 대한 초기화를 완료했으니 구면 좌표계에서 직교 좌표계로 변환하는 메소드도 만들어보자

이 또한 위키 백과에 변환 수식이 잘 설명되어 있어 그 내용을 그대로 들고 와 적용해 본다.

$\theta$ => 앙각(Elevation)
$\phi$ => 방위각(Azimuth)

\[x=r\\sin(\\theta)\\cos(\\phi)\] \[y=r\\cos(\\theta)\] \[z=r\\sin(\\theta)\\sin(\\phi)\]

  
 public class SphericalCoordinate
{
 	public Vector3 ToCartesianPosition()
    {
        return new Vector3(
            _radius * Mathf.Sin(Elevation) * Mathf.Cos(Azimuth),
            _radius * Mathf.Cos(Elevation),
            _radius * Mathf.Sin(Elevation) * Mathf.Sin(Azimuth));
    }
}

3. 한 바퀴 돌리기

어쌔신 크리드의 동기화처럼 카메라를 한 바퀴 돌려주기 위해서 방위각에 360을 더해 돌려줄 것이다.

나머지는 코드를 통해 알아보자!

  
public class SphericalCoordinate
{
    public IEnumerator AzimuthRotate(Transform target,float duration,Action updateCallBack = null, Action endCallBack = null)
    {
        float time = 0.0f;

        float startAzimuth = Azimuth;
        while(time < 1f)
        {
            Azimuth = Mathf.Repeat(
            	Mathf.Lerp(startAzimuth, startAzimuth + (360f * Mathf.Deg2Rad), time)
            	, _maxAzimuthAngle - _minAzimuthAngle);
            target.position = ToCartesianPosition();
            updateCallBack?.Invoke();
            time += Time.deltaTime / duration;
            yield return null;
        }

        endCallBack?.Invoke();
    }
}

360f * Mathf.Deg2Rad
삼각 함수로 인해 방위각(Azimuth)이 라디안 값이 되었으므로 360도 또한 라디안 값으로 바꿔줘야 한다.
Mathf.Repeat
방위각(Azimuth)이 0(_minAzimuthAngle) ~ 360(_maxAzimuthAngle)를 반복적으로 돌 수 있게 Repeat 처리한다
updateCallBack
회전하면서 계속 처리해줘야 할 내용을 콜백 메소드로 처리
endCallBack
모든 행동이 끝난 뒤에 처리해줘야 할 내용을 콜백 메소드로 처리

4. 결과

구면 좌표계를 실제로 적용해 보는 것에 중점을 두고 만든 것이다 보니 많이 부족해 보인다.

위 코드로는 월드 좌표계의 원점을 기준으로만 회전이 가능하나 코드 수정을 통해 원점을 이동시켜 수정이 가능하다.

사용을 해보니 딱 느껴진 것은 “3인칭 게임 카메라 구현을 구면 좌표계를 이용해서 하면 되겠다!!”였다. 보통 3인칭 게임에서 카메라가 이동할 수 있는 범위가 구면 좌표계 범위와 동일하고 반지름을 통해 줌 인 줌 아웃도 구현할 수 있을뿐더러 방위각, 앙각, 반지름을 조절해서 다양한 카메라 워킹을 구현할 수 있기 때문이다.

2023.05.16 추가

구면 좌표계를 이용하여 “3인칭 게임 카메라 움직임”을 구현해 보았습니다!

[Unity] 구면 좌표계로 3인칭 카메라 움직임 구현하기

추가로 찾아보니 구면 좌표계를 이용해서 구체 곡면을 이동하는 캐릭터 움직임을 만들 수도 있었는데 나중에 이것도 만들어보고 정리를 해볼 생각이다.

참고 내용

https://ko.wikipedia.org/wiki/%EA%B5%AC%EB%A9%B4%EC%A2%8C%ED%91%9C%EA%B3%84

구면좌표계 - 위키백과, 우리 모두의 백과사전