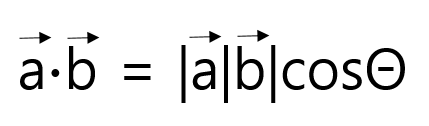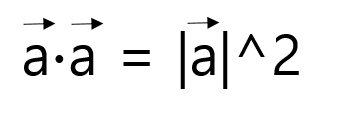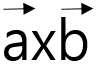정의
- 유클리드 벡터(Euclidean Vector) 또는 벡터(Vector)는 유클리드 공간에서 크기와 방향을 모두 포함하는 기하학적 대상
기하학적 의미의 벡터
- 벡터는 위치가 중요하지 않다 왜냐하면 위치가 바뀌여도 벡터의 크기와 방향이 변하지 않기 때문
- 즉, 두 벡터가 길이가 같고 같은 방향을 가르킬 때 두 벡터는 상등(Equal)하다 라고 할 수 있다
벡터의 연산
벡터의 덧셈
- 벡터의 덧셈은 두 벡터를 결합하여 새로운 벡터를 만든다
- AB벡터 + BC벡터 = AC벡터
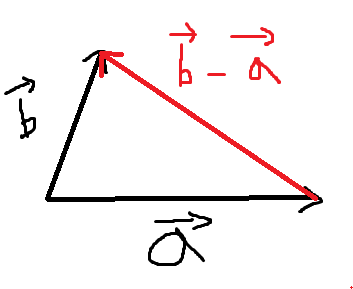
벡터의 뺄셈
- 두번 째 벡터의 종점에서 첫번 째 벡터의 종점으로 이어진다.
벡터의 내적
- a벡터와 b벡터가 이루는 각이 Θ일 때, 두 벡터의 크기와 두 벡터가 이루는 각의 코사인 값을 곱으로 계산
벡터의 내적 특징
- 내적의 결과는 스칼라 값이다. 따라서 내적을 연속해서 계산할 수 없다.
- 두 벡터 중 하나가 영벡터일 때 내적의 값은 0이다. ( 영벡터의 크기가 0이기 때문 )
- 동일한 벡터끼리의 내적은 벡터 크기의 제곱이다.
- 두 벡터가 이루는 각이 90도(수직) 이면 내적의 값은 0이다.
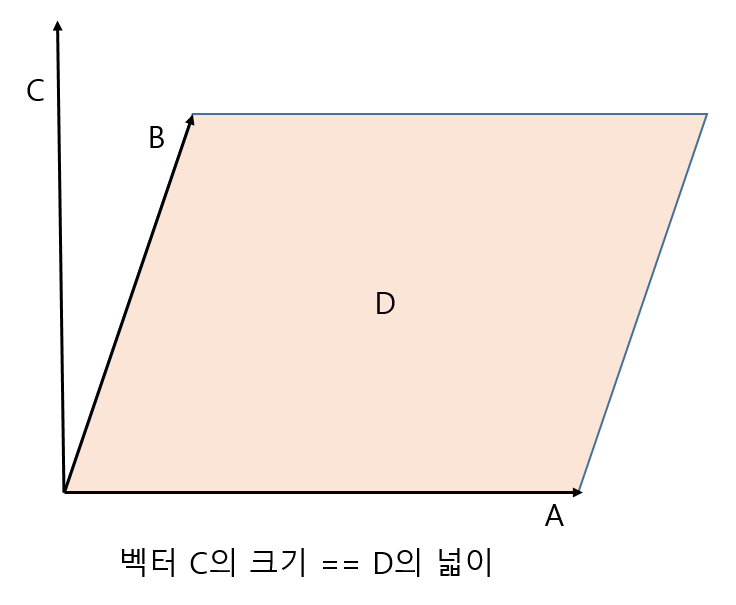
벡터의 외적
(a cross b 라 읽는다. )
- 결과 값은 벡터이다.
- 결과 벡터의 방향 : 두 벡터에 동시에 수직인 방향
- 결과 벡터의 크기 : a벡터와 b벡터 크기를 변으로하는 평행사변형의 넓이
- 법선 벡터 == 벡터의 외적